Die Streckgrenze eines Werkstoffs ist ein Maß für die ertragbaren mechanischen Spannungen. Wenn diese die Streckgrenze überschreiten, setzt Fließen und somit Plastifizierung ein. Die Streckgrenze spielt bei Werkstoffen zur Dimensionierung eines Bauteils eine wichtige Rolle. Üblicherweise werden die Werte für die Streckgrenze eines Werkstoffs Tabellenwerken entnommen. Diese werden in der Regel mit dem genormten Zugversuch ermittelt, mit dem die Spannungs-Dehnungs-Kurve bestimmt wird. Jedoch weichen diese Werte von den tatsächlichen eines realen Bauteils ab und dies teilweise erheblich. Zum einen unterliegen die Festigkeitseigenschaften eines Werkstoffs chargenbedingt entsprechenden Toleranzen. Zum anderen weist das reale Bauteil ein durch die Wärmebehandlung und Fertigungsverfahren entstandenes Gefüge auf, was sich nicht in den Ergebnissen aus den Zugversuchen für einen bestimmten Werkstoff wiederfindet. Hier bietet die instrumentierte Eindringprüfung die Möglichkeit, an den realen Bauteilen die tatsächliche Streckgrenze zu bestimmen. Zudem ist erfolgt diese am Bauteilrand, was insbesondere bei Tribosystemen vorteilhaft ist, weil diese Zone die Größe der ertragbaren Kontaktspannungen bestimmt.
1 Instrumentierte Eindringprüfung
Bei der instrumentierten Eindringprüfung werden während eines Belastungs- und Entlastungsvorgangs des Eindringkörpers die Prüfkraft und die Eindringtiefe kontinuierlich gemessen. Je nach Größenordnung wird diese als Mikroindentierung (Mikrohärteprüfung) oder als Nanoindentierung bezeichnet. Eine weitere übliche Bezeichnung ist Martens-Härteprüfung nach Adolf Martens, der die Härteprüfung definiert hat als eine Prüfung zum Bestimmen des Widerstands, den ein Werkstoff der dauerhaften Verformung durch Eindringen eines härteren Eindringkörpers entgegensetzt. Aus der gemessenen Kraft-Weg-Kurve werden die Härte und weitere Materialkennwerte zur Charakterisierung der Festigkeitseigenschaften des Materials bestimmt (Abb. 1).

Abb. 1: Verlauf der Prüfkraft über die Eindringtiefe und Werte, die aus dem Kurvenverlauf bestimmt werden
Als Eindringkörper wird entweder eine vierseitige Vickers-Pyramide oder bei der Nanoindentierung eine dreiseitige Berkovich-Pyramide verwendet. Diese weist im Gegensatz zum Vickers-Eindringkörper keine Dachkante auf. Deshalb ist sie sehr gut für kleinste Eindringtiefen geeignet, da sie eine echte Spitze hat. Aufgrund der sehr kleinen Eindringtiefen kann die Prüfung als quasi zerstörungsfrei betrachtet werden.
2 Spannungs-Dehnungs-Kurve durch Eindringprüfung
Bei einem Berkovich-Eindringkörper sind die Dehnungen e durch den Eindringvorgang nahezu unabhängig von der Eindringtiefe h. Um durch diese Prüfung aber die Streckgrenze bestimmen zu können, bedarf es eines funktionalen Zusammenhangs zwischen Eindringtiefe h beziehungsweise Dehnung e und der Spannung s. Diese Forderung erfüllt die Kugel als Eindringkörper, denn bei dieser ist die Dehnung e proportional der Eindringtiefe h und somit besteht ein funktionaler Zusammenhang mit der Spannung s, der im elastischen Bereich linear ist (Abb. 2).

Abb. 2: Verlauf von Spannung und Dehnung für die vorteilhafte Form des Eindringkörpers
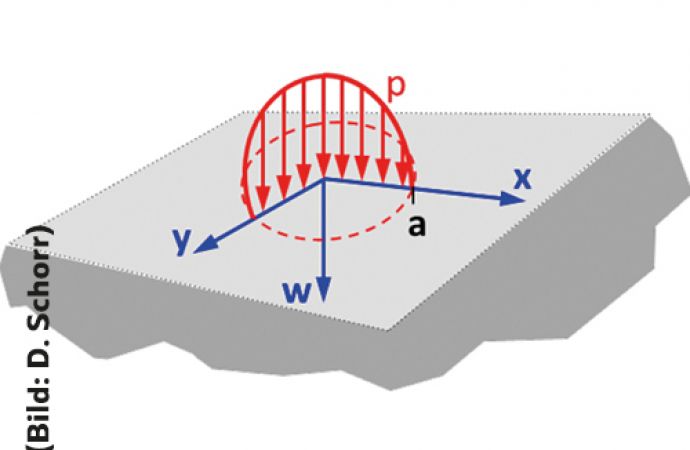
3 Hertz’sche Kontaktspannungen sphärischer Eindringkörper
In der Praxis wird der Prüfkörper für die Ermittlung der Spannungs-Dehnungs-Kurve nicht als vollständige Kugel, sondern als Kegel mit sphärischer Oberfläche und einem sehr kleinen Radius ausgeführt. Hierbei haben sich Radien in der Größenordnung von 10 µm bis 50 µm als vorteilhaft erwiesen. Die beim Eindringen entstehenden Spannungen pmax hängen gemäß den Hertz‘schen Kontaktgleichungen vom Radius R ab (Abb. 3).

Abb. 3: Verdeutlichung der auftretenden Spannungen gemäß der Hertz'schen Kontaktgleichungen
Da es nahezu unmöglich ist, eine sphärische Oberfläche mit einem über die Fläche konstanten Radius in der Größenordnung von 10 µm bis 50 µm herzustellen, muss der tatsächliche Radius durch Messungen bestimmt werden. Erst dann kann mit dem Eindringkörper die Spannungs-Dehnungs-Kurve bestimmt werden. Dazu wird der sogenannte effektive Radius Reff in Abhängigkeit der Eindringtiefe h bestimmt. Dazu ist es vorteilhaft, die Prüfkraft ansteigend mit lokalen Maxima und Minima zu erhöhen (Abb. 4). Dieser Verlauf der Prüfkraft wird als kontinuierlicher Multizyklusmodus bezeichnet (Continous Multicycle = CMC).

Abb. 4: Messverfahren CMC
Aus diesen Messungen wird unter Zuhilfenahme der Hertz‘schen Kontaktgleichungen mit dem reduzierten E-Modul Er der effektive Radius des Eindringkörpers bestimmt (Abb. 5). Wie man aus diesen Messergebnissen sehr schön entnehmen kann, ist der tatsächliche Radius nicht konstant für verschiedene Eindringtiefen h und nähert sich erst mit zunehmender Eindringtiefe dem nominalen Radius. Dieser beträgt bei dem verwendeten Eindringkörper 20 µm.

Abb. 5: Bestimmung des effektiven Radius Reff aus einer CMC-Messung
4 Streckgrenze durch Eindringprüfung
Damit liegen nun die Voraussetzungen vor, um mit der instrumentierten Eindringprüfung die Spannungs-Dehnungs-Kurve s = f(e) für einen Werkstoff zu ermitteln und daraus die Streckgrenze Re zu bestimmen. Ein typisches Verfahren besteht darin, die Prüfkraft progressiv mit einer überlagerten Sinusfunktion zu steigern und dadurch für jeden Sinuszyklus einen Messpunkt zu erhalten (Abb. 6).

Abb. 6: Verlauf der Prüfkraft mit überlagerter Sinusfunktion

Abb. 7: Spannungs-Dehnungs-Kurve an einer Stahlprobe durch instrumentierte Eindringprüfung
Die Prüfung an einer Stahl-Zugprobe mit zertifizierter Streckgrenze führt zu dem in Abbildung 7 dargestellten Zusammenhang zwischen Spannung und Dehnung. Die Streckgrenze Reergibt sich am Schnittpunkt der beiden Ausgleichsgeraden.
Abbildung 8 zeigt den Vergleich der durch die instrumentierte Eindringprüfung ermittelten Werte für die Streckgrenze Re mit dem zertifizierten Wert einer Stahl-Zugprobe. Es ist deutlich zu erkennen, dass das Verfahren für Stahl sehr gute Werte liefert. Die Abweichungen zum zertifizierten Wert sind deutlich geringer als Standardwerte aus Zugversuchen für einen bestimmten Werkstoff, die sich bis zu 20 % vom Wert des realen Bauteils unterscheiden können.

Abb. 8: Vergleich der Streckgrenzen Re an Stahl-Zugproben
5 Fazit
Durch die Instrumentierte Eindringprüfung in der Ausführung als Nanoindentierung steht ein Verfahren zur Verfügung, welches in der Lage ist, den tatsächlichen Wert für die Streckgrenze eines Bauteils zu ermitteln, ohne dazu gesonderte Zugproben anfertigen zu müssen. Hierzu wird vorteilhafterweise ein sphärischer Eindringkörper verwendet mit einem Radius im Bereich von 10 µm bis 50 µm. Um die Fertigungsungenauigkeiten des Radius zu berücksichtigen und um eine ausreichende Genauigkeit des Messverfahrens zu erreichen, wird der tatsächliche effektive Radius des sphärischen Prüfkörpers durch Messungen bestimmt. Dieser geht dann in die Hertz’schen Kontaktgleichungen ein, die zur Berechnung der Spannungs-Dehnungs-kurve dienen.
Kontakt
Steinbeis Transferzentrum Tribologie in Anwendung und Praxis, Erzbergerstraße 121, D-76133 Karlsruhe
- www.steinbeis-analysezentrum.com